频域特征指标及其MATLAB代码实现¶

以前我们梳理过常用的有量纲时域特征指标和无量纲时域特征指标，其实特征提取方法中，一些频谱特征指标也是十分有用的。

下述频域特征指标是根据信号的功率谱求得的。在故障诊断或者其他应用场景下，可以与时域指标以及其他指标一同作为特征向量的一部分，丰富特征量种类，提升诊断正确率。

功率谱¶

下述频域特征都是在功率谱基础上计算求得的，但是为什么不用频谱呢？个人认为是因为功率谱在表达功率信号乃至随机信号频域特征时更具有普适性，毕竟功率信号就不能用频谱表示。

1 重心频率¶

重心频率能够描述信号在频谱中分量较大的信号成分的频率，反映信号功率谱的分布情况。换句话说，对于给定的频带范围，低于重心频率的频率范围内包含的能量是信号总能量的一半。

另一种理解方式，重心频率是以功率谱的幅值为权值的加权平均，所以重心频率会向功率谱幅值更大（即权值更大）的位置移动。

更形象一点，如果把下图中功率谱曲线围起来的区域看作一块木板，那么当把这块木板放在重心频率虚线所在的钢丝上时，木板刚好能保持平衡。

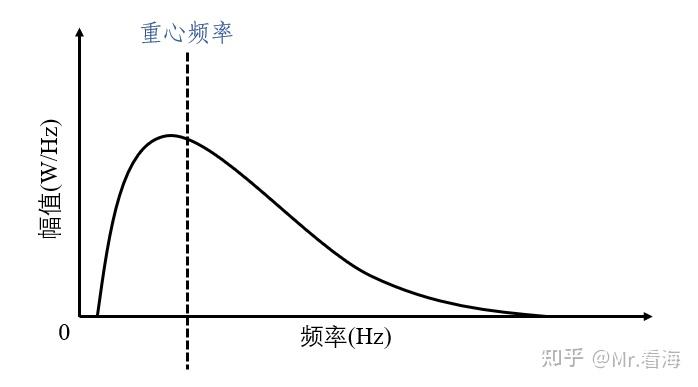
重心频率公式：

2 均方根频率¶

均方根频率就是均方频率的算数平方根，它也有一个辅助理解的物理含义：如果把下图中功率谱曲线围起来的区域看作一块木板，那么当这块木板围绕y轴旋转时，均方根频率所在位置到原点的距离就是旋转体的惯性半径（指物体质量假设的集中点到转动轴间的距离）。

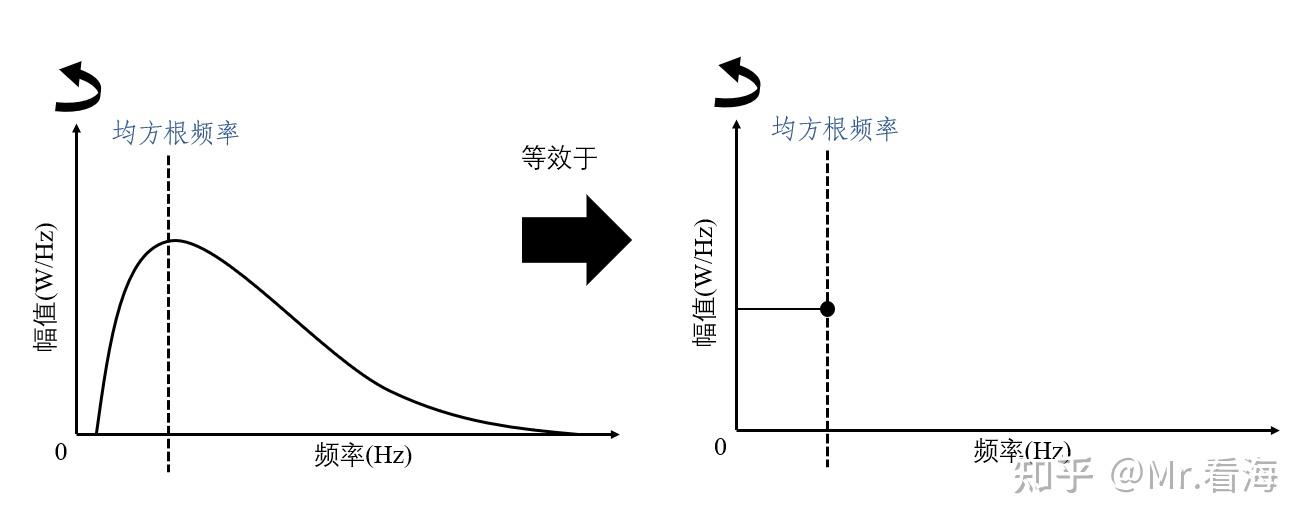
均方频率公式：

3 均方频率¶

均方频率是均方根频率的平方。

与重心频率不同，均方频率是信号频率平方的加权平均，同样以功率谱的幅值为权。

重心频率、均方频率、均方根频率都是描述功率谱主频带位置分布的。

4 频率标准差¶

同样把下图中功率谱曲线围起来的区域看作一块木板，频率标准差就是重心频率为中心的惯性半径。

若重心附近的频谱幅值较大，则频率标准差较小；若重心附近的频谱较小，则频率标准差较大。 频率标准差用于描述功率谱能量分布的分散程度。

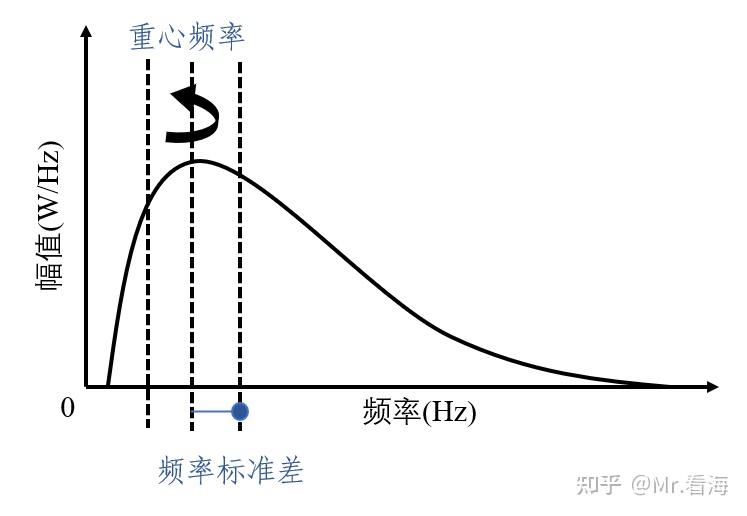
频率标准差公式：

5 频率方差¶

频率方差就是频率标准差的平方，是衡量功率谱能量分散程度的另一个度量维度。就不过多描述了。

频率方差公式：